في هذه المحاضرة، سننفذ 3 أوراق بحثية، [2] Mnih، إلخ. التحكم على مستوى الإنسان من خلال التعلم التعزيزي العميق، [3] Hasselt، إلخ. التعلم التعزيزي العميق باستخدام التعلم Q المزدوج و [4] Wang، إلخ. بنيات الشبكة المتضاربة للتعلم التعزيزي العميق .

لكن قبل ذلك، سنعود إلى المحاضرة الأخيرة حيث نقدم تقريب الوظيفة والتعلم العميق Q. كما ننفذ [1] Mnih، إلخ. لعب Atari مع التعلم التعزيزي العميق 2013. في هذه المحاضرة سنعمل على تحسين خوارزمية DQN لتحقيق أداء أفضل.

تم إصلاح DQN

البديل الأول لـ DQN يسمى Fixed-DQN من [2] Mnih، إلخ. ورقة التحكم على مستوى الإنسان من خلال التعلم التعزيزي العميق ، في هذه الورقة يقدم المؤلفون تعديلًا بسيطًا على الورقة السابقة [1] . نظرًا لأن التعلم التعزيزي معروف بأنه غير مستقر أو حتى يتباعد عندما يتم استخدام مقرب دالة غير خطية مثل الشبكة العصبية لتمثيل دالة قيمة الفعل (المعروفة أيضًا باسم Q). هذا عدم الاستقرار له عدة أسباب:

• الارتباطات الموجودة في تسلسل الملاحظات، وحقيقة أن التحديثات الصغيرة لـ Q قد تغير السياسة بشكل كبير وبالتالي تغير توزيع البيانات
• الارتباطات بين قيم الفعل (Q) وقيم الهدف 𝑟 + 𝛾𝑚𝑎𝑥 ₐ ′ 𝑄 ( 𝑠 ′, 𝑎 ′)

بالنسبة للمشكلة الأولى، قمنا بحلها في المحاضرة السابقة باستخدام مخزن إعادة التشغيل الذي يقوم بالتوزيع العشوائي للبيانات، وبالتالي إزالة الارتباطات في تسلسل الملاحظة وتنعيم التغييرات في توزيع البيانات

بالنسبة للثاني، استخدمنا تحديثًا تكراريًا يضبط قيم الفعل (Q) نحو قيم الهدف التي يتم تحديثها بشكل دوري فقط، وبالتالي تقليل الارتباطات مع الهدف. بدلاً من استخدام نموذج واحد للتنبؤ بالهدف وقيمة Q للحالة الحالية، يقوم المؤلف بإنشاء نموذجين (شبكات عصبية عميقة) بهياكل متطابقة. واستخدام واحد للتنبؤ بالهدف والآخر لتعلم قيمة Q.

في المحاضرة السابقة، دالة الخسارة لدالة 𝑄 − 𝑙𝑒𝑎𝑟𝑛𝑖𝑛𝑔 هي:

𝐿 ( 𝜃ᵢ )= 𝐸 [( 𝑟 + 𝛾𝑚𝑎𝑥 ₐ ′ 𝑄 ( 𝑠 ₙₑₓₜ ، 𝑎 ′ ، 𝜃ᵢ )− 𝑄 ( 𝑠 ، 𝑎 ، 𝜃ᵢ ))²]

حيث أن 𝑟 + 𝛾𝑚𝑎𝑥 ₐ ′ 𝑄 ( 𝑠𝑛𝑒𝑥𝑡 , 𝑎 ′, 𝜃ᵢ ) هو الهدف و𝜃ᵢ هو معامل النموذج والتوقع يأخذ فقط متوسط ​​الخسارة على مدى تدريب دفعة واحدة. كما يمكننا أن نلاحظ في المعادلة (1) أن النموذج الذي يتنبأ بالهدف وقيمة Q هو نفسه. سنستخدم نموذجين بدلاً من نموذج واحد، ثم نقوم بتحديث نموذج الهدف لكل خطوة 𝐾 .

هل تساعد هذه الفكرة في تقليل الضوضاء؟

إجابة:

تتكون أي مشكلة تعلم خاضعة للإشراف من أزواج [( 𝑥 1، 𝑦 1)، ( 𝑥 2، 𝑦 2)،…( 𝑥𝑛 ، 𝑦𝑛 )]∼ 𝐷

حيث كل زوج هو مثال تدريبي من التوزيع 𝐷 الذي نريد تقديره. إذا كان 𝑦 ثابتًا، فإذا قمنا بتدريب مقدر جيد (يعتمد على البيانات والمشكلة والحل المطلوب وما إلى ذلك) فسوف نقترب من التوزيع الحقيقي أو سنكون قريبين جدًا منه. مشكلة RL هي التسمية 𝑦 ، وهي تتغير بمرور الوقت، لذلك إذا استخدمنا المفهوم السابق، فسيظل الهدف 𝑦 ثابتًا لـ (خطوة k)، مما يجعل التدريب أكثر استقرارًا وكفاءة من ذي قبل.

يتم استخدام تدوين الخوارزمية الجديدة: 𝑄 ( 𝑠 , 𝑎 , 𝜃ᵢ ⁻ ) للتنبؤ بالهدف بينما يتم استخدام 𝑄 ( 𝑠 , 𝑎 , 𝜃ᵢ ⁺ ) لتعلم 𝑄 − 𝑣𝑎𝑙𝑢𝑒

الوظيفة. سوف نطلق على النموذج الأول اسم نموذج الهدف والثاني اسم النموذج المتصل بالإنترنت .

تصبح دالة الخسارة:

𝐿 ( 𝜃ᵢ ⁺ )= 𝐸 [( 𝑟 + 𝛾𝑚𝑎𝑥 ₐ ′ 𝑄 ( 𝑠 ₙₑₓₜ ، 𝑎 ′ ، 𝜃ᵢ ⁻ )− 𝑄 ( 𝑠 ، 𝑎 ، 𝜃ᵢ ⁺ ))²]

وفي كل 𝑘 خطوة نقوم بتحديث النموذج المستهدف باستخدام النموذج عبر الإنترنت ، 𝑄 ( 𝜃 ⁻ )← 𝑄 ( 𝜃 ⁺ ) نقوم بتعيين معلمات النموذج المستهدف بحيث تساوي معلمة النموذج عبر الإنترنت في كل 𝑘 خطوة:

سنقوم الآن بتحديث الكود من المحاضرة السابقة.

𝑁𝑜𝑡𝑒 :

سوف نقوم فقط بتحرير فئة DQN_Agent، وسوف أشير إلى سطر التحرير بواسطة علامة ⟶.

يمكنك استخدام الكود الكامل هنا.

#هذا النموذج موصى به من ورقة "Mnih et al.، 2015؛ van Hasselt et al.، 2015" 
keras.backend.clear_session()النموذج = keras.Sequential ([ 
    keras.layers.Conv2D (32، 8، strides = 4، padding = 'صالح'، التنشيط = 'relu'، شكل الإدخال = [84، 84، 4])، 
    keras.layers.Conv2D (64، 4، strides = 2، padding = 'صالح'، التنشيط = 'relu')، 
    keras.layers.Conv2D (64، 3، strides = 1، padding = 'صالح'، التنشيط = 'relu')، 
    keras.layers.Flatten ()، 
    keras.layers.Dense (512، التنشيط = 'relu')، 
    keras.layers.Dense (مساحة العمل) 
]) 
نموذج. الملخص ()

التغيير الأول هو أن هيكل النموذج هو تغيير صغير ولكنه يحدث فرقًا.

الفئة Fixed_DQN_Agent: 
    self.online_model=model 
    self.target_model=keras.models.clone(model) 
    self.target_model.set_weights(model.get_weights())

التغيير الثاني، لدينا نموذجان بدلاً من نموذج واحد، online_model و target_model ، الأول يستخدم لحساب دالة 𝑄 − 𝑣𝑎𝑙𝑢𝑒 في كل خطوة زمنية بينما الآخر يحسب الهدف فقط. يحتوي نموذج الهدف على نفس بنية النموذج عبر الإنترنت ونفس المعلمة الأولية.

معدل التحديث الذاتي=خطوات التحديث

تحديث آخر للخوارزمية السابقة، حيث نحتاج إلى معلمة تحدد معدل التحديث للنموذج المستهدف.

def _epsilon_greedy_policy(self,state,epsilon): 
        if np.random.rand()<epsilon: 
            return np.random.randint(self.action_space) 
        else: 
#----> هنا نستخدم النموذج عبر الإنترنت للتنبؤ بأفضل إجراء. 
            Q_values=self.online_model.predict(state[np.newaxis]) 
            return tf.argmax(Q_values[0])

نظرًا لأن لدينا نموذجين الآن، فنحن بحاجة إلى استخدام النموذج عبر الإنترنت في سياسة 𝜖 − 𝑔𝑟𝑒𝑒𝑑𝑦 لأنه النموذج الذي يقدر الدالة 𝑄 − 𝑣𝑎𝑙𝑢𝑒 .

def _training_step(self): 
    # الحصول على الدفعة من replay_buffer (ذاكرتنا) 
    states,actions,rewards,dones,next_states=self._sample_experiences() 
#----> the online_Q(state,a)=online_Q(state,a) + alpha [ reward + gamma * max (target_Q(next_state,a) for all a) - online_Q(state,a)] 
    next_Q_values=self.target_model.predict(next_states) 
    max_next_Q_values=np.max(next_Q_values,axis=1) 
    # حساب الهدف الذي هو [reward + gamma * max(target_Q(next_state,a) over a)] 
    target_Q_values=rewards+(1-dones)*self.discount_factor*max_next_Q_values#هذا القناع مهم لإخفاء قيمة الإجراءات التي لا نستخدمها، فهو عبارة عن مصفوفة ثنائية الأبعاد بقيمة 1 إذا تم اختيار الإجراء الأول وصفر إذا تم اختيار الإجراء الآخر. 
    mask = tf.one_hot(actions, self.action_space)#ابدأ تسجيل التدرج لحساب التدرج لنموذجنا. 
    مع tf.GradientTape() كشريط: 
#----> احسب دالة Q للحالة الحالية (هنا للدفعة بأكملها). 
        all_Q_values=self.online_model(states) 
        #هنا نستخدم القناع حتى نقوم بتقليل النتيجة للإجراء الذي اخترناه فقط. 
        Q_values=tf.reduce_sum(all_Q_values*mask,axis=1,keepdims=True) 
        #احسب دالة الخسارة مع الهدف الذي نحسبه في المقام الأول. 
        loss=tf.reduce_mean(self.loss_function(target_Q_values,Q_values)) 
#----> احسب التدرج لمعامل online_model الخاص بنا. 
    gradiants=tape.gradient(loss,self.online_model.trainable_variables) 
#----> قم بتطبيق خطوة التحسين باستخدام التدرج الذي نحسبه للنموذج عبر الإنترنت 
    self.optimizer.apply_gradients(zip(gradiants,self.online_model.trainable_variables))

تحتوي وظيفة training_step أيضًا على بعض التغييرات، حيث يتنبأ النموذج المستهدف الآن بالهدف. بينما عندما أجرينا خطوة التحسين قمنا بتحديث معلمة النموذج عبر الإنترنت .

def fit(self): 
    # 
    # جميع الأسطر متشابهة 
    #-----> هنا حيث يتم تحديث نموذج الهدف بعد 100 حلقة عن طريق تعيين المعلمة كنموذج متصل بالإنترنت. 
    إذا كانت الحلقة%self.update_rate: 
        self.target_model.set_weights(self.online_model.get_weights())

التحديث الأخير موجود في دالة الملاءمة حيث نقوم بتحديث النموذج المستهدف بعد 𝑘 خطوة عن طريق تعيين معلماته كنموذج متصل بالإنترنت

التعلم Q المزدوج

إن التعلم الثابت Q هو تقريبًا ولكن مع تغيير بسيط في من يتنبأ بالهدف. إنه سؤال مفتوح عما إذا كان هذا يؤثر سلبًا على الأداء في الممارسة العملية إذا حدث المبالغة في التقدير . إن تقديرات القيمة المفرطة في التفاؤل ليست بالضرورة مشكلة في حد ذاتها. إذا كانت جميع القيم أعلى بشكل موحد، فسيتم الحفاظ على تفضيلات العمل النسبية ولن نتوقع أن تكون السياسة الناتجة أسوأ. علاوة على ذلك، من المعروف أنه من الجيد أحيانًا أن نكون متفائلين. التفاؤل في مواجهة عدم اليقين هو أسلوب استكشاف معروف Kaelbling et al.، 1996. ومع ذلك، إذا لم تكن المبالغة في التقدير موحدة ولم تركز على الحالات التي نرغب في معرفة المزيد عنها، فقد تؤثر سلبًا على جودة السياسة الناتجة. يقدم Thrun وSchwartz، 1993 أمثلة محددة حيث يؤدي هذا إلى سياسات دون المستوى الأمثل، حتى بشكل مقارب. بسبب تحيز التعظيم عندما نستخدم Fixed-DQN نحصل على مقدر تحيز بسبب اختيار التعظيم . وفقا لـ Sun و Tsitsiklis، 2007 حتى لو كان المقدر غير متحيز، فإن اتخاذ الإجراء الأقصى يؤدي إلى سياسة التحيز.

على سبيل المثال: لنفترض أن الحالة الفردية 𝑀𝐷𝑃 (| 𝑆 |=1) بها فعلان ( 𝑎 ₁, 𝑎 ₂)، وكلا الفعلين لهما 0 مكافأة متوسطة. [𝔼( 𝑟 | 𝑎 = 𝑎 ₁)=𝔼( 𝑟 | 𝑎 = 𝑎 ₂)=0]. عندئذٍ، 𝑄 ( 𝑠 , 𝑎 ₁)= 𝑄 ( 𝑠 , 𝑎 ₂)=0= 𝑉 ( 𝑠 ) لنقدر 𝑄 ̂ ( 𝑠 , 𝑎 ₁)، 𝑄 ̂ ( 𝑠 , 𝑎 ₂). استخدم مقدرًا غير متحيز لـ 𝑄 : على سبيل المثال 𝑄 ̂ =(1/ 𝑛) ∑ ᵢ 𝑟ᵢ ( 𝑠 ، 𝑎 ₁) حيث 𝑛 هو عدد مرات اتخاذ الإجراء 𝑎 ₁. دع 𝜋 ̂ = 𝑎𝑟𝑔𝑚𝑎𝑥 ₐ 𝑄 ̂ ( 𝑠 ، 𝑎 ₁) تكون السياسة الجشعة. على الرغم من أن كل تقدير لقيم الحالة-الإجراء غير متحيز، فإن تقدير 𝜋 ̂ 𝑣𝑎𝑙𝑢𝑒𝑉 ̂ 𝜋 متحيز.

𝑝𝑟𝑜𝑜𝑓 :

𝑉 ̂ =𝔼[ 𝑚𝑎𝑥 ( 𝑄 ( 𝑎 ₁ ), 𝑄 ( 𝑎 ₂))]

≥ 𝑚𝑎𝑥 𝔼[ 𝑄 ( 𝑎 ₁ )، 𝑄 ( 𝑎 ₂)]

= 𝑚𝑎𝑥 [0,0]

=0

= 𝑉𝜋

يمكننا أن نلاحظ في السطر الثاني أن القيمة المقدرة ≥ أكبر من القيمة الحقيقية .

الفكرة وراء خوارزمية التعلم Q المزدوجة فان هاسلت، 2010 ، والتي تم اقتراحها لأول مرة في إعداد جدولي، تقدم حلاً لهذه المشكلة المسماة التعلم Q المزدوج . الفكرة هي كما يلي، تقسيم العينات واستخدامها لإنشاء تقديرين مستقلين غير متحيزين لـ 𝑄 ₁ ( 𝑠 ، 𝑎ᵢ )، 𝑄 ₂ ( 𝑠 ، 𝑎ᵢ )؛ ∀ 𝑎

• استخدم تقديرًا واحدًا لاختيار الحد الأقصى للإجراء 𝑎 *= 𝑎𝑟𝑔𝑚𝑎𝑥 ₐ 𝑄 ₁ ( 𝑠 , 𝑎 )
• استخدم تقديرًا آخر لتقدير قيمة 𝑎 *: 𝑄 ₂ ( 𝑠 , 𝑎 *)
• يعطي تقديرًا غير متحيز: 𝔼( 𝑄 ₂ ( 𝑠 , 𝑎 *))= 𝑄 ₂ ( 𝑠 , 𝑎 *)

يمكن تعميم هذه الفكرة للعمل مع التقريب الوظيفي التعسفي، بما في ذلك الشبكات العصبية العميقة.

في القسم السابق، قدمنا ​​Fixed_DQN وأظهرنا أن الهدف يتبع المعادلة (2)، وكما هو موضح في [3] ، سنتوقع الهدف باستخدام المعادلة التالية.

𝑌 ᴰᵒᵘᵇˡᵉ = 𝑅 ₜ₊₁ + 𝛾𝑄 ( 𝑠 ₙₑₓₜ ، 𝑎𝑟𝑔𝑚𝑎𝑥 ₐ 𝑄 ( 𝑠 ₙₑₓₜ ، 𝑎 ، 𝜃 ⁺)، 𝜃 ⁻)

حيث 𝑄 (; 𝜃 ⁻) هو النموذج المستهدف و 𝑄 (; 𝜃 ⁺)

هو النموذج على الانترنت .

لاحظ أن اختيار الإجراء في argmax لا يزال يرجع إلى الأوزان عبر الإنترنت 𝜃 ⁺.

كما هو الحال في Q-learning ، ما زلنا نقدر قيمة السياسة الجشعة وفقًا للقيم الحالية، كما هو محدد بواسطة 𝜃 ⁺. ومع ذلك، نستخدم المجموعة الثانية من الأوزان 𝜃 ⁻ لتقييم قيمة هذه السياسة بشكل عادل. يمكن تحديث هذه المجموعة الثانية من الأوزان كما هو الحال في القسم السابق (كل خطوة 𝑘 ).

سنقوم بتحديث وكيل Fixed_DQN ويمكنك الحصول على الكود الكامل.

def _training_step(self): 
    # الحصول على الدفعة من replay_buffer (ذاكرتنا) 
    states,actions,rewards,dones,next_states=self._sample_experiences() 
#----> the online_Q(state,a)=online_Q(state,a) + alpha [ reward + gamma * target_Q(next_state,argmax online_Q(next_state,a_i) for all a)-online_Q(state,a)] 
#----> كما نرى هنا نستبدل التنبؤ من نموذج الهدف بالنموذج عبر الإنترنت كما يوصي "Hado van Hasselt 2015" 
    next_Q_values=self.online_model(next_states) 
#----> هنا نتخذ أفضل إجراء على كل الإجراءات للدفعة بأكملها      
    best_action=np.argmax(next_Q_values,axis=1) 
#----> إنشاء قناع لتقليل قيمة الإجراءات أننا لا نستخدم         
    best_action_mask = tf.one_hot(best_action, self.action_space).numpy()#----> احسب الهدف الذي هو [المكافأة + جاما * target_Q(next_state,argmx online_Q(next_state,a) over a) ]     
    max_next_Q_values=(self.target_model(next_states) * next_mask).sum(axis=1) 
    target_Q_values=rewards+(1-dones) * self.discount_factor * max_next_Q_values 
    ​​# 
    #الباقي هو نفسه كما كان من قبل

المبارزة DDQN

الفرق الوحيد في Dueling-DDQN هو بنية النموذج وليس الخوارزمية في ورقة Ziyu Wang وما إلى ذلك. 2016 تظهر أن التغيير الطفيف في بنية النموذج يتفوق على الخوارزمية القديمة، لذا فإننا نتوقع بدلاً من ذلك 𝑄 ( 𝑠 ، 𝑎 )

مباشرة، نتوقع أولاً 𝑉 ( 𝑠 ) و𝐴 ( 𝑠 , 𝑎 ) حيث 𝐴 ( 𝑠 , 𝑎 ) هي الميزة كما هو موضح في Birds 1993

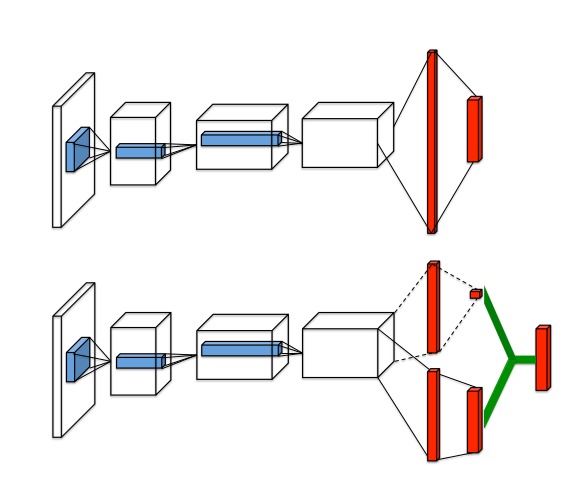
حيث، 𝐴 ( 𝑠 ، 𝑎 ) = 𝑄 ( 𝑠 ، 𝑎 )- 𝑉 ( 𝑠 ) حيث تقيس دالة القيمة 𝑉 مدى جودة أن تكون في حالة معينة 𝑠 . ومع ذلك، تقيس الدالة 𝑄 قيمة اختيار إجراء معين عند التواجد في هذه الحالة. تطرح دالة الميزة 𝐴 قيمة الحالة من دالة Q للحصول على مقياس نسبي لأهمية كل إجراء. نقوم بتصميم بنية شبكة Q واحدة ، كما هو موضح في الشكل 1، والتي نشير إليها باسم شبكة المبارزة . الطبقات السفلية من شبكة المبارزة ملتوية كما هو الحال في DQNs الأصلية (Mnih et al.، 2015) . ومع ذلك، بدلاً من متابعة الطبقات الملتوية بتسلسل واحد من الطبقات المتصلة بالكامل، نستخدم بدلاً من ذلك تسلسلين (أو تيارين) من الطبقات المتصلة بالكامل. يتم إنشاء التدفقات بحيث يكون لديها القدرة على توفير تقديرات منفصلة لوظائف القيمة والميزة. أخيرًا، يتم دمج التدفقين لإنتاج خرج واحد Q.

𝑄 ( 𝑠 , 𝑎 ) = 𝑉 ( 𝑠 ) + 𝐴 ( 𝑠 , 𝑎 )

𝑉 ( 𝑠 ) هو خرج المقياس، لذا فإن خرج التدفق لهذا الفرع يحتوي على خلية عصبية واحدة للإخراج، بينما 𝐴 ( 𝑠 , 𝑎 ) يحتوي على أكبر عدد من الإجراءات المتاحة لدينا، لذا فإن خرج هذا التدفق يحتوي على | 𝐴𝑐𝑡𝑖𝑜𝑛𝑠 | خلية عصبية.

ومع ذلك، يجب أن نضع في الاعتبار أن 𝑄 ( 𝑠 , 𝑎 ) هو تقدير معلمي فقط لدالة Q الحقيقية . علاوة على ذلك، سيكون من الخطأ استنتاج أن 𝑉 ( 𝑠 ) مقدر جيد لدالة قيمة الحالة ، أو على نحو مماثل أن 𝐴 ( 𝑠 , 𝑎 ) يوفر تقديرًا معقولًا لدالة الميزة

المعادلة أعلاه غير قابلة للتحديد بمعنى أنه نظرًا لـ 𝑄 لا يمكننا استرداد 𝑉 و𝐴 بشكل فريد. لرؤية ذلك، أضف ثابتًا إلى 𝑉 ( 𝑠 ) واطرح نفس الثابت من 𝐴 ( 𝑠 ، 𝑎 ). يلغي هذا الثابت ما ينتج عنه نفس قيمة 𝑄 . ينعكس هذا الافتقار إلى القدرة على التحديد في الأداء العملي الضعيف عند استخدام هذه المعادلة مباشرة. لمعالجة مشكلة القدرة على التحديد هذه، يمكننا إجبار مقدر دالة الميزة على أن يكون له ميزة صفرية عند الإجراء المختار. أي أننا نسمح للوحدة الأخيرة من الشبكة بتنفيذ التعيين الأمامي

𝑄 ( 𝑠 , 𝑎 ) = 𝑉 ( 𝑠 ) + ( 𝐴 ( 𝑠 , 𝑎 ) − الحد الأقصى ₐ 𝐴 ( 𝑠 , 𝑎 ))

الآن، بالنسبة إلى 𝑎 * = 𝑎𝑟𝑔𝑚𝑎𝑥 ₐ 𝑄 ( 𝑠 , 𝑎 ) = 𝑎𝑟𝑔𝑚𝑎𝑥 ₐ 𝐴 ( 𝑠 , 𝑎 )

نحصل على 𝑄 ( 𝑠 , 𝑎 *)= 𝑉 ( 𝑠 ). وبالتالي، يوفر التدفق 𝑉 ( 𝑠 ) تقديرًا لدالة القيمة، بينما ينتج التدفق الآخر تقديرًا لدالة الميزة. تستبدل وحدة نمطية بديلة عامل max بمتوسط:

𝑄 ( 𝑠 , 𝑎 )= 𝑉 ( 𝑠 )+[ 𝐴 ( 𝑠 , 𝑎 )−(1/| 𝐴 |)∑ ₐ 𝐴 ( 𝑠 , 𝑎 )]

من ناحية أخرى، يفقد هذا الدلالات الأصلية لـ 𝑉 و 𝐴

لأنها أصبحت الآن بعيدة عن الهدف بمقدار ثابت، ولكن من ناحية أخرى فإنها تزيد من استقرار التحسين: مع المعادلة الأخيرة، تحتاج المزايا فقط إلى التغيير بنفس سرعة المتوسط، بدلاً من الاضطرار إلى تعويض أي تغيير في ميزة الإجراء الأمثل، لذلك سننفذ المعادلة الأخيرة على نموذجنا.

هندسة النموذج هي نفسها كما هو موضح في Mnih وما إلى ذلك 2015، Hasselt وما إلى ذلك 2015 ولكن مع تيار من طبقة متصلة بالكامل.

#هذا النموذج موصى به من ورقة "Ziyu Wang et al., 2016" 
# لبناء النموذج، سنستخدم واجهة برمجة التطبيقات Functinal من keras. 
keras.backend.clear_session()المدخلات = keras.layers.Input(الشكل=[84,84,4]) 
x=keras.layers.Conv2D(32,8,strides=4,padding='صالح',التنشيط='relu')(المدخلات) 
x=keras.layers.Conv2D(64,4,strides=2,padding='صالح',التنشيط='relu')(x) 
x=keras.layers.Conv2D(64,3,strides=1,padding='صالح',التنشيط='relu')(x)   
x=keras.layers.Flatten()(x)V_h1=keras.layers.Dense(512, التنشيط='relu')(x) 
A_h1=keras.layers.Dense(512, التنشيط='relu')(x)قيمة الحالة=keras.layers.Dense(1)(V_h1)الميزة الخام = keras.layers.Dense (مساحة العمل) (A_h1)الميزة = raw_advantage-tf.reduce_mean(raw_advantage,axis=1,keepdims=True)قيمة Q=tf.add(الميزة، قيمة الحالة)النموذج=keras.Model(المدخلات=[المدخلات]، المخرجات=[قيمة_Q])نموذج.ملخص()

ثم استخدم DDQN_Agent السابق دون أي تغيير على الإطلاق، ويمكنك الحصول على الكود الكامل من Github