عمليات اتخاذ القرار ماركوف وخوارزمية النموذج الأساسي

في أوائل القرن العشرين، درس عالم الرياضيات أندريه ماركوف العمليات العشوائية التي لا تعتمد على الذاكرة، والتي تسمى سلاسل ماركوف.
تحتوي مثل هذه العملية على عدد ثابت من الحالات (محدود)، وتتطور بشكل عشوائي من حالة إلى أخرى في كل خطوة.

احتمالية
تطوره من حالة s إلى حالة s' ثابتة، وتعتمد فقط على الزوج (s, s')، وليس على الحالات الماضية (لهذا السبب نقول أن النظام ليس لديه ذاكرة)

مثال على سلسلة ماركوف.

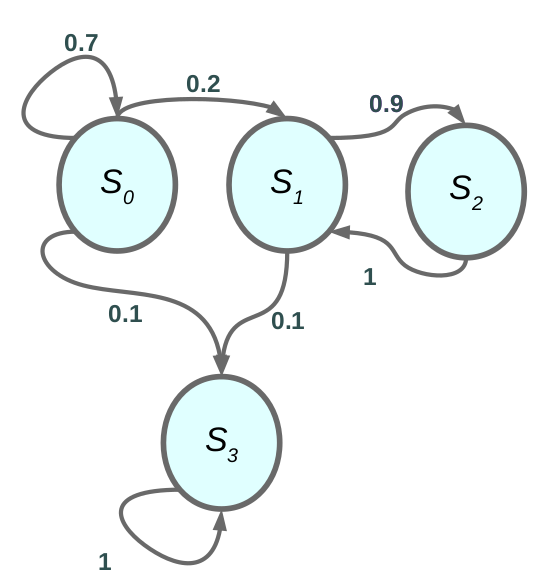
تقول خاصية ماركوف أن الحالة الحالية كافية لتمثيل تاريخ العالم بأكمله.

ص (سₜ₊₁ |سₜ، أₜ) = ص (سₜ₊₁ |حₜ) … (1)

في المعادلة (1) تمثل hₜ التاريخ الكامل من الخطوة الأولى حتى خطوة الوقت الحالية. وكما قلنا سابقًا أن الانتقال من حالة إلى أخرى يعتمد فقط على الحالة الحالية، في عالم آخر تمثل الحالة الحالية التاريخ الكامل.

مثال:
سيارة ذاتية القيادة، الحالة الحالية كافية للوكيل لمعرفة الإجراء الذي يجب اتخاذه.
دون التفكير في مدى تعقيد الحالة الحالية للسيارة المجاورة، والمشاة، والضوء، والمحرك، وما إلى ذلك ...
ولكن إذا قمت بتمثيل كل هذه الميزات في متجه واحد يمثل الحالة الحالية، فإن هذا المتجه (الحالة) يكفي لاتخاذ الإجراء.

عمليات ماركوف

كما هو الحال في الشكل 1، فإن MP عبارة عن سلسلة من الحالات ذات خاصية ماركوف. التعريف الكامل.

1. مجموعة منتهية من الحالات
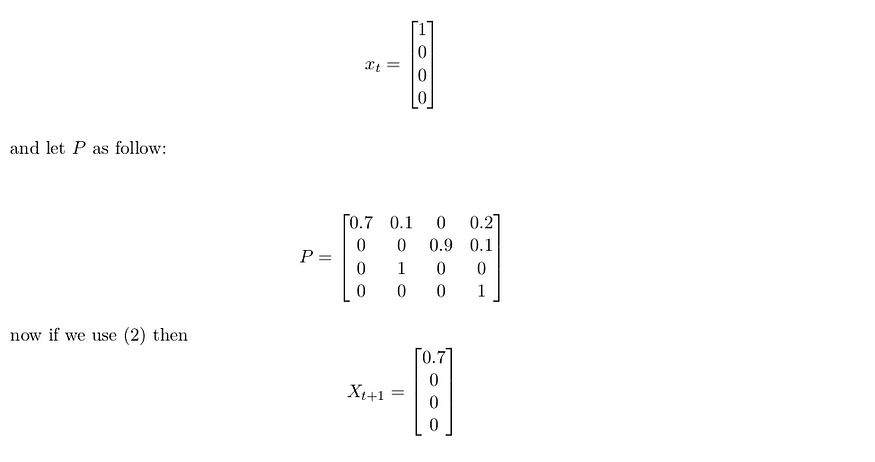
2. P هو نموذج ديناميكي للعالم P (s ₜ = s ′ |sₜ= s) لنسمي المتجه X ₜ هو تمثيل الحالة في خطوة الوقت t والمصفوفة P هي النموذج الديناميكي مع البعد NxN وN هو عدد الحالات

X ₜ₊₁ = P ∗ Xₜ … (2)

حيث ∗ هو حاصل الضرب النقطي

مثال: تحتوي مساحة الحالات على 4 حالات ونمثل كل حالة كمتجه ساخن واحد كما هو موضح في الشكل 1

عمليات مكافأة ماركوف

في MRP، نقوم بإجراء تحريف بسيط، حيث نضيف دالة المكافأة إلى سلسلة ماركوف،
ولا يزال لدينا نموذج ديناميكي كما كان من قبل ولكن مع دالة المكافأة.
تعريف MRP:

1. S هي مجموعة منتهية من الحالات (s ∈ S)
2. P هو نموذج ديناميكي يحدد P(s ₜ₊₁ = s|s ₜ= s ′ )
3. R هي دالة المكافأة R(sₜ= s) = E[rₜ |sₜ = s]
4. γ هو عامل الخصم γ ∈ [0, 1]

دالة المكافأة إذا كنت في حالة معينة فما هي المكافأة المتوقعة التي تحصل عليها من تلك الحالة؟ وعامل الخصم γ يسمح لنا بالتفكير في مقدار وزن المكافآت الفورية مقابل مكافآت الميزة.
الآن بعد أن نضيف المكافأة إلى العالم، يمكننا تعريف العائد والعائد المتوقع كما في السابق، نحدد العائد على النحو التالي.

Gₜ= Rₜ+ γRₜ₊₁ + γ²Rₜ₊₂ + · · · (3)

V = E[Gₜ|sₜ= s] = E[rₜ+ γrₜ₊₁+ γ²rₜ₊₂ + · · · |sₜ= s] … (4)

في الشكل 2 يمكننا رؤية عمليات ماركوف مع المكافآت في كل حالة والانتقال على القوس.

ملحوظة :

1. إذا كانت العمليات حتمية، فإن G t وV متماثلان، ولكن إذا كانت العمليات عشوائية، فسوف تكون مختلفة
2. إذا كانت أطوال الحلقة محدودة دائمًا، فيمكنك استخدام γ = 1

حساب قيمة MRP.

1. يمكن التقدير عن طريق المحاكاة: إنشاء عدد كبير من الحلقات، ومتوسط ​​العائد، وحساب العائد المتوقع.
2. إذا كان العالم ماركوفيًا، فيمكننا تحليل دالة القيمة في
   V (s) = R(s) + γ ∑ P (s ′ |s) V (s ′ ) … (5)

إذا كنا في حالة MRP منتهية، فيمكننا كتابة V (s) باستخدام تدوين المصفوفة.

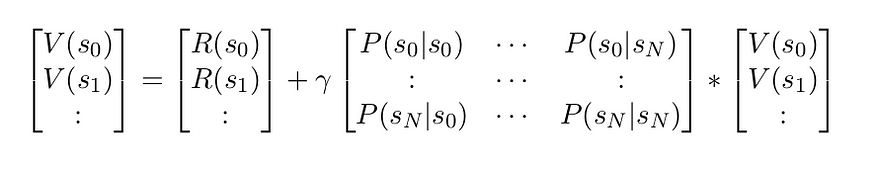
V = R + γP V … (6)

حيث أن المتجه V و R يحتويان على N عنصر و P عبارة عن مصفوفة ذات شكل NxN .
يمكننا حل (6) باستخدام الجبر الخطي.

V − γP V = R
V (I − γP ) = R
V = (I − γP ) ⁻ ¹R

لحل هذه المعادلة نحتاج إلى عملية O(N³) لحساب معكوس المصفوفة، إذا كانت N كبيرة فإن الأمر غير قابل للتنفيذ. لحسن الحظ، يمكننا حل المشكلة باستخدام الخوارزمية التكرارية.

3. خوارزمية تكرارية باستخدام البرمجة الديناميكية
أ. تهيئة V (s) = 0 لجميع s.
ب. بالنسبة إلى k = 1 حتى التقارب:
لجميع s ∈ S:
Vₖ(s) = R(s) + γ ∑ ₛ ′ P (s ′ |s)Vₖ₋₁ (s ′ )

التعقيد الحسابي هو O(N²) حيث N هو عدد الحالات.

عمليات اتخاذ القرار ماركوف

تم وصفها لأول مرة في الخمسينيات من القرن العشرين بواسطة ريتشارد بيلمان. وهي تشبه سلاسل ماركوف ولكن مع وجود اختلاف: في كل خطوة، يمكن للوكيل اختيار أحد الإجراءات الممكنة العديدة، وتعتمد
احتمالات الانتقال على الإجراء المختار. علاوة على ذلك، فإن بعض انتقالات الحالة تعيد بعض المكافأة (إيجابية أو سلبية)، وهدف الوكيل هو إيجاد سياسة من شأنها تعظيم المكافأة بمرور الوقت.
إنها مجرد MRP + الإجراءات
تعريف MDP.

1. S هي مجموعة منتهية من الحالات (s ∈ S)
2. أ هي مجموعة من الأفعال أ ∈ أ
3. P هو نموذج ديناميكي لكل إجراء يحدد P(sₜ₊₁ = s|sₜ = s ′ , aₜ=a)
4. R هي دالة المكافأة R(sₜ= s, aₜ= a) = E[rₜ|sₜ= s, aₜ= a]
5. γ هو عامل الخصم γ ∈ [0, 1]

MDP عبارة عن مجموعة (S, A, P, R, γ)

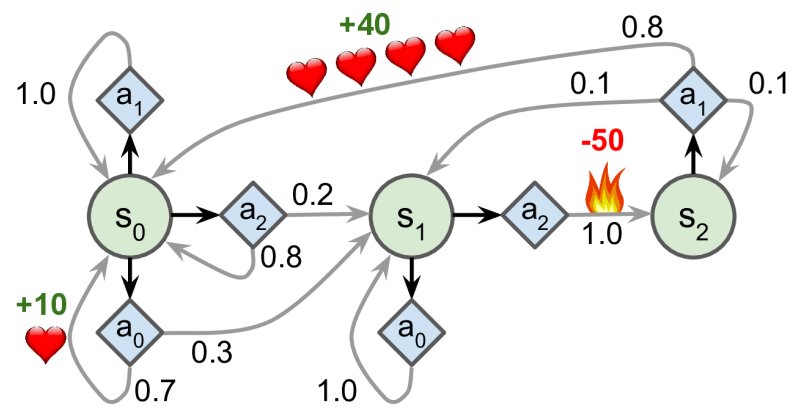
كما قلنا في المقالة السابقة، تحدد السياسة الإجراء الذي يجب اتخاذه في كل حالة. π(a|s) = P (aₜ= a|sₜ= s)
إذا أضفنا سياسة إلى MDP فإننا نعود إلى MRP وهذه خاصية مهمة للغاية لأنه يمكننا الآن استخدام تقنية الحساب لـ MRP مع MDP إذا كنا نستخدم بعض السياسات. هذا صحيح لأنك تحدد توزيعك على الإجراء.

Rπ (s) =∑ₐ π(a|s)R(s, a)

Pπ (s′ |s) = ∑ₐ π(a|s)P (s ′ |s, a)

خوارزمية تقييم السياسات

1. قم بتهيئة V (s) = 0 لجميع s.
   2. بينما صحيح:
   لجميع s ∈ S:
   V ₖ(s) = R(s, π(s)) + γ ∑ₛ ′ π (s ′ ) P (s ′ |s, π(s))Vₖ₋₁
   |Vᵢ− Vᵢ ₊₁ | < ϵ break

هذا هو نسخة احتياطية لسياسة معينة.

يتحكم

نحن لا نريد فقط تقييم السياسة، بل نريد أن نتعلم سياسة جيدة، وهنا يأتي دور التحكم في
حساب السياسة المثلى:

π*= argmax_π V … (7)

في المعادلة أعلاه نأخذ السياسات الكلية القصوى التي تجعل دالة القيمة هي الحد الأقصى قدر الإمكان. أحد الخيارات هو البحث عن حساب السياسة المثلى، عدد السياسات الحتمية هو |A|ˢ حيث |A| هو عدد الإجراءات و|S| هو عدد الحالات.

إن تكرار السياسة يكون أكثر كفاءة بشكل عام.

خوارزمية تكرار السياسة
1. خوارزمية تكرار السياسة باستخدام البرمجة الديناميكية
1. تعيين i = 0
2. تهيئة π 0 (s) عشوائيًا لجميع s.
3. بينما صحيح:
Vπᵢ = تقييم السياسة على πᵢ
πᵢ ₊₁ = تحسين السياسة
i + = 1
|πᵢ− πᵢ ₊₁ | < ϵ break.

لقد رأينا بالفعل خوارزمية تقييم السياسة ولكن ماذا عن تحسين السياسة قبل أن نكتب الكود الزائف لتحسين السياسة، سنقدم دالة مهمة جدًا تسمى دالة الحالة-الفعل. تحسب هذه الدالة قيمة كل حالة تتخذ إجراءً، لذا نحسب القيمة لكل زوج (s، a).

Q π (s, a) = R(s, a) + γ ∑ₛ ′ P (s ′ |s, a) Vπ (s ′ ) … (8)

تحسين السياسة
خوارزمية تحسين السياسة
1. بالنسبة إلى s ∈ S,a ∈ A:
2. Q πᵢ (s, a) = R(s, a) + γ ∑ ₛ ′ P (s ′ |s, a)V πᵢ(s ′ )
3. πᵢ ₊₁ = argmax ₐQπ لجميع s ∈ S
4. إرجاع πᵢ ₊₁

فلماذا هذا العمل؟
من تحسين السياسة نقول أن πᵢ₊₁ = argmax_a Qπ لجميع s ∈ S ماذا تعني هذه المعادلة، إذا اتخذت الحد الأقصى للإجراء لحالة واحدة ثم باتباع السياسة القديمة، فأنا متأكد من أنني أقوم بتحسين أو على الأقل استخدام السياسة السابقة، إذا اتخذت الحد الأقصى للإجراء الإجمالي لكل حالة، فأنا أضمن أن هذه السياسة الجديدة أفضل من السياسة السابقة. الحد الأقصى للإجراء هو
دالة قيمة الحالة من التعريف.

الحد الأقصى Q π ᵢ (s, a) = R(s, a) + γ ∑ₛ ′P (s ′ |s, a)V π ᵢ (s ′ ) = V π ᵢ (s)

نحن نرفض أن يكون تحسين السياسة تحسنًا رتيبًا. أي ما يعني؛ ∀s ∈ S؛ V πᵢ ≤ V πᵢ+1

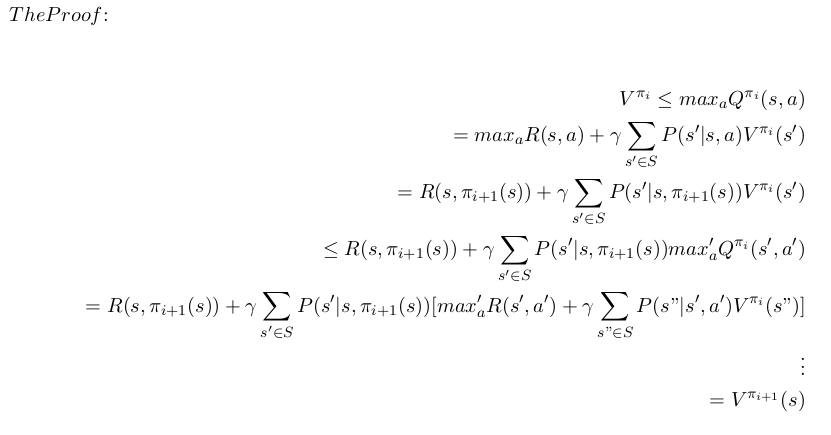
لقد قمنا بتوسيع التعريف حتى وصلنا إلى تعريف V π i+1
والشيء الأخير الذي سنتحدث عنه هو خوارزمية تكرار القيمة والتي هي التقارب كتكرار للسياسة ولكن مع جوانب مختلفة.

تكرار القيمة.

دعنا نحدد مشغلي النسخ الاحتياطي لـ Bellman

BV(s) = max ₐ R(s, a) + γ ∑ₛ ′P (s ′ |s, a)V (s ′ )

BV يعطي دالة قيمة على جميع الحالات s

خوارزمية تكرار القيمة
1. تعيين K = 1
2. تعيين V (s) = 0؛ ∀s ∈ S.
3. بينما صحيح:
بالنسبة إلى s ∈ S:
Vₖ₊₁ (s) = max ₐ R(s, a) + γ ∑ₛ ′P (s ′ |s, a)Vₖ(s ′ )

|Vₖ− Vₖ₊₁ | = 0 انقطاع.

إذا استخدمنا عرض النسخ الاحتياطي لـ Bellman:
V ₖ₊₁ = BVₖ

تعمل الخوارزمية على النحو التالي نبدأ ونقوم بتهيئة $V(s) = 0 $ ثم نكرر حتى نتقارب،
في الأساس لكل حالة نقوم بعمل نسخة احتياطية لـ Bellman. لذلك بالنسبة للنسخة الاحتياطية الأولى، نأخذ أقصى مكافأة فورية وهي الأفضل إذا كان لدينا خطوة واحدة للقيام بها، ثم نستمر في النسخ الاحتياطي في عالم آخر ما هي أفضل خطوة يجب القيام بها إذا كان عليّ اتخاذ خطوتين أو ثلاث خطوات وما إلى ذلك. على سبيل المثال، إذا كنت مبتدئًا في لعبة الشطرنج، فإنني أجد أفضل حركة يجب اتخاذها دون تفكير في السيناريو المستقبلي، ولكن عندما أتدرب واكتسب الخبرة، يمكنني القيام بحركة أفضل من خلال محاكاة التحركات التالية
التي يمكن أن تحدث على اللوحة.

إثبات تقارب تكرار القيمة.
دع O عاملًا، و |x| معيارًا لـ x، إذا كان |OX − OX ′ | ≤ |X − X ′ | فإن O هو عامل انكماش. O هي دالة في التفكير التحليلي ومصفوفة في الجبر، لذا دعنا نقول أن V و V ′ عبارة عن متجهين ونضرب كل منهما في المصفوفة O إذا كانت O عملية انكماش فإن المسافة (المعيارية)
بين هذين المتجهين تصبح أصغر.

النظرية : عامل بيلمان هو عامل انكماش إذا كانت γ < 1.
الإثبات:
دع |V − V ′ | = max ₛ|V (s) − V (s ′)| هو معيار اللانهاية

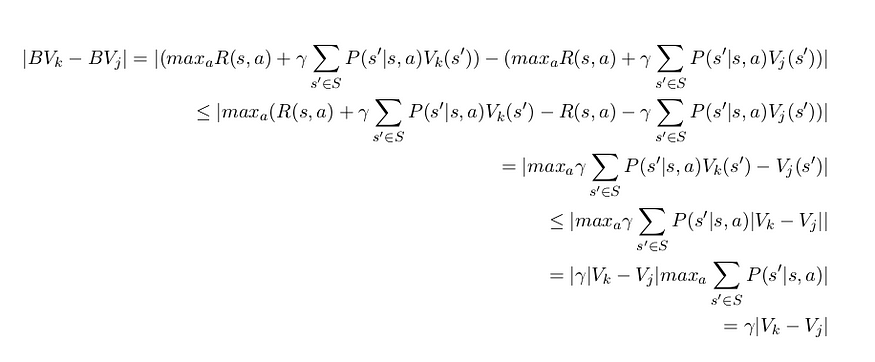
لذا، حتى لو كانت جميع المتباينات متباينات، فهذا لا يزال انكماشًا إذا كانت γ < 1.

ملخص

في هذه المقالة نقدم عمليات اتخاذ القرار لماركوف وخوارزمية قاعدة النموذج، والتي تستخدم للعثور على أفضل إجراء للقيام به في بعض المواقف (الحالة) إذا كنا نعرف النموذج الديناميكي (نموذج العالم). نقدم خوارزمية تكرار السياسة وتكرار القيمة والتي عندما نثبت تتقارب إلى السياسة المثلى إذا قمت بتشغيل الخوارزمية لفترة زمنية كافية. في المقالة التالية سنقدم خوارزمية النموذج الحر حيث يمكنني تعلم دالة القيمة وليس التخطيط فقط.

آمل أن تجد هذه المقالة مفيدة وأنا آسف للغاية إذا كان هناك أي خطأ أو خطأ إملائي في المقالة، فلا تتردد في الاتصال بي، أو ترك تعليق لتصحيح الأمور.

خليل حنارة
مهندس ذكاء اصطناعي في مسراج