تنفيذ التعلم الآلي في شكل جدول

في هذه المقالة سوف نقوم بتنفيذ إحدى الخوارزميات التي ذكرناها من قبل، وفي رأيي هذه هي أفضل طريقة للحصول على كافة تفاصيل الخوارزمية.

أفترض أنك على دراية بالفعل بالترميز ولغة برمجة Python ، لذلك إذا كنت لا تعرف أساسيات الترميز والبايثون، فلن تتمكن من متابعة هذه المقالة.

لفهم أفضل حاول إعادة كتابة الكود بنفسك وليس مجرد قراءته.
يمكنك تنزيل الكود الكامل من مستودع GitHub هنا .

هذه هي المقالة الأولى التي نستخدم فيها الكود في هذه الدورة لذلك سنحاول أن نبقيه بسيطًا قدر الإمكان، في هذه المقالة نستخدم لعبة Frozenlake .
كما هو الحال بالنسبة لمعظم ألعاب الشبكة، فإن الدور بسيط للغاية أحتاج إلى عبور البحيرة دون الوقوع في الحفر.

كما نرى في الشكل أعلاه يوجد نوعان من الكتل، الكتلة * المجمدة * التي يمكنني عبورها و *الثقب * الذي يؤدي إلى الموت.

في هذه المقالة، سوف نقوم بتنفيذ الكود الكامل من البداية بينما في مقال لاحق سوف نستخدم إطار عمل يجعل الحياة أسهل، لذا فلنبدأ.

أولاً، دعنا نستورد التبعيات. كما ذكرنا من قبل، سننفذ الكود من الصفر، سنحتاج إلى numpy والذي يجب أن تكون على دراية به إذا لم تقرأ الفصلين الأولين من [3] وهو مورد جيد جدًا ليس فقط لتعلم الكود ولكن أيضًا لتعلم مفاهيم التعلم الآلي. الآن سننفذ البيئة. كما هو الحال في الشكل 2، سنمثل اللعبة كشبكة ثنائية الأبعاد، بالنسبة للكتلة المجمدة سنمثلها باستخدام حرف F و H للثقوب و S لموضع البداية و G للهدف.

كما نقول في المقال الأول لإطار التعلم التعزيزي العام، نحتاج إلى وكيل وبيئة للتفاعل معها ونمثل الوكيل في البيئة بالحالة والقيمة أو الفائدة من القيام ببعض الإجراءات في تلك الحالة بالمكافأة . لذلك نحتاج إلى إسقاط مشكلتنا على هذا الإطار.

• الوكيل هو اللاعب الذي يقوم بالتحرك على الشبكة.
• الحالة هي موضع الوكيل في الوقت الحالي t .
• المكافأة هي 1 إذا عبر العميل البحيرة (وصل إلى الهدف) و0 إذا لم يفعل و-1 إذا خسر (سقط في الحفرة )

كل مشكلة تحتاج إلى نمذجتها بطريقة تساعد على حلها. واحدة من أصعب المهام هي إيجاد دالة مكافأة جيدة تقود عمليات التعلم كما ذكرنا في المحاضرة الأولى.
هذه المشكلة في شكل حلقات، مما يعني أن كل لعبة تمثل حلقة واحدة وفي كل حلقة لدينا العديد من الخطوات، ولكل حلقة هناك حالة ذات طرفين وهي الفوز أو الخسارة لذلك ستنتهي كل حلقة بعد عدد من الخطوات.
الآن يمكننا أن نبدأ الكود.

نحن نعرف البيئة كفئة تسمى FrozenLake و init هو المنشئ ونعرف لوحة اللعبة كلوحة ثابتة من أجل البساطة ولكن يمكنك محاولة جعلها قابلة للتغيير.
* pos * هو الموضع الحالي و * N * هو بُعد اللوحة و * actions_rep * هو فقط لإظهار مؤشر الإجراء.

وظيفة إعادة الضبط هي لإعادة ضبط اللعبة إلى الحالة الأولية ونحن بحاجة إلى استدعاء هذه الوظيفة في كل مرة نحتاج فيها إلى بدء لعبة جديدة.

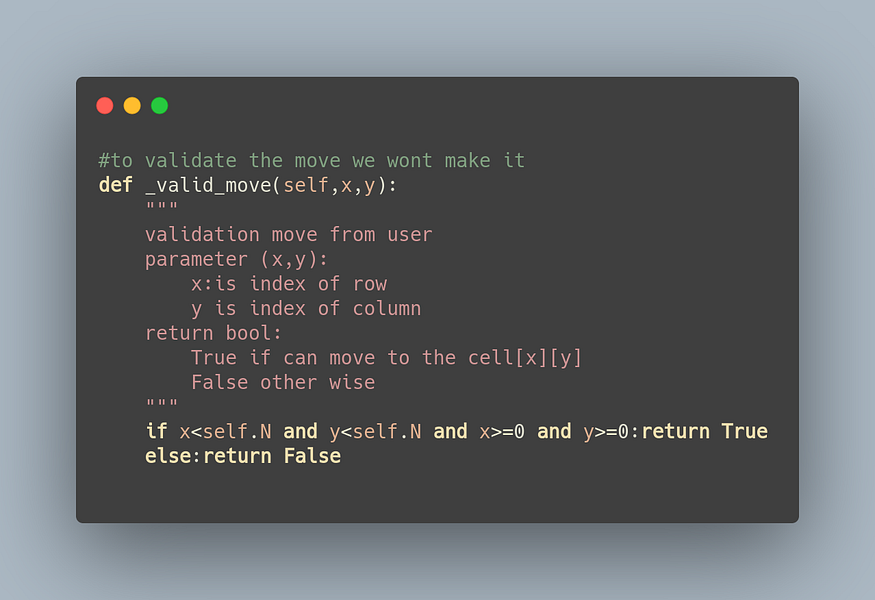
في valid_move يتم التحقق مما إذا كان الإجراء صالحًا، يكون الإجراء صالحًا إذا وفقط إذا حدث على الملل، لذلك إذا قمت بإجراء يؤدي إلى خارج الحدود، فهذه ليست خطوة صالحة.

#هذا واحد ينشئ الخطوة ويعيد obs،reward،done 
def step(self،action): 
        """ 
        هذه الوظيفة تتخذ إجراءً وتعيد ضبط حالة 
        معلمة اللعبة: 
            action=range(4) 
            {0:Up،1:Down،2:right،3:left} 
        return :(state،reward،done) 
            state:الحالة الجديدة في النطاق [0،15] 
            reward 0 إذا لم يكن كذلك، قم بالإنهاء -1 إذا خسر 1 إذا وصلنا إلى الهدف 
            تم القيام به خطأ بينما لم يكن كذلك (فوز أو خسارة) 
        """ 
        reward=-1 
        تم القيام به=خطأ 
        إذا كان الإجراء==0: 
            #اذهب للأعلى 
            if self._valid_move(self.pos[0]-1، self.pos[1]): 
                if self.grid[self.pos[0]-1][self.pos[1]]=='H': 
                    reward=-1 
                    تم القيام به=صحيح 
                elif self.grid[self.pos[0]-1][self.pos[1]]=='G': 
                    reward=1 
                    تم = صحيح 
                وإلا: 
                    المكافأة = 0 
                    تم = خطأ 
                self.grid[self.pos[0]-1][self.pos[1]]='*' 
                self.pos[0]-=1 
        elif action==1: 
            #اذهب للأسفل 
            إذا كان self._valid_move(self.pos[0]+1,self.pos[1]): 
                إذا كان self.grid[self.pos[0]+1][self.pos[1]]=='H': 
                    المكافأة = -1 
                    تم = صحيح 
                elif self.grid[self.pos[0]+1][self.pos[1]]=='G': 
                    المكافأة = 1 
                    تم = صحيح 
                وإلا: 
                    المكافأة = 0 
                    تم = خطأ 
                self.grid[self.pos[0]+1][self.pos[1]]='*' 
                self.pos[0]+=1 
        elif action==2: 
            #اذهب لليمين 
            إذا كان self._valid_move(self.pos[0],self.pos[1]+1): 
                إذا self.grid[self.pos[0]][self.pos[1]+1]=='H': 
                    reward=-1 
                    done=True 
                elif self.grid[self.pos[0]][self.pos[1]+1]=='G': 
                    reward=1 
                    done=True 
                else: 
                    reward=0 
                    done=False 
                self.grid[self.pos[0]][self.pos[1]+1]='*' 
                self.pos[1]+=1 
        elif action==3: 
            #اذهب إلى اليسار 
            if self._valid_move(self.pos[0],self.pos[1]-1): 
                if self.grid[self.pos[0]][self.pos[1]-1]=='H':
                    المكافأة=-1
                    تم = صحيح 
                elif self.grid[self.pos[0]][self.pos[1]-1]=='G': 
                    reward=1 
                    تم = صحيح 
                وإلا: 
                    reward=0 
                    تم = خطأ 
                self.grid[self.pos[0]][self.pos[1]-1]='*' 
                self.pos[1]-=1 
        return (self.pos[0]*self.N+self.pos[1]),reward,done

دالة الخطوة هي الأهم حيث ننفذ منطق اللعبة. تعيد هذه الدالة الحالة الجديدة والمكافأة وما إذا كانت اللعبة قد انتهت أم لا. الحالة التالية هي الموضع الجديد للاعب، والمكافأة هي 1 إذا فزنا و 0 إذا لم نفز بعد، و-1 إذا خسرنا. تساعدنا الدالة done في تنفيذ التعلم Q. في المحاضرة السابقة، قلنا أنه إذا أدت الخطوة التي قمنا بها إلى نهاية الحلقة، فإن قيمة حالة الإجراء هذه هي المكافأة الفورية فقط لأنه لا يوجد إجراء تالٍ يمكننا القيام به.

def render(self): 
        """ 
        اطبع لوحة اللعبة 
        """ 
        لـ i في self.grid: 
            print(i)

الوظيفة الأخيرة في فئة FrozenLake هي وظيفة العرض التي تطبع اللوحة التي تمثل الموضع الحالي للوكيل كـ '*'

بعد أن قمنا بتنفيذ البيئة سوف نقوم الآن بكتابة مكونات الوكيل.

def exploration_policy(epsilon,state,q_tabel): 
    """ 
    هذه الوظيفة مخصصة لإجراءات عشوائية، 
    نستخدم سياسة إبسيلون لإجراءات عشوائية، 
    نرجع رقمًا صحيحًا من [0,3] يشير إلى الإجراء 
    """ 
    if np.random.rand()<epsilon: 
        return np.random.randint(1,4) 
    else: 
        return np.argmax(q_tabel[state])

المكون الأول هو السياسة التي نحددها وهي سياسة 𝜖 − 𝑔𝑟𝑒𝑒𝑑𝑦 يمكنك القراءة عن نموذج هذه السياسة في المحاضرة السابقة.

#inite جدول Q_value حيث يكون الصف هو الحالة والعمود هو الإجراء، يمكننا القيام بـ 
Q_tabel=np.zeros((16,4))

Q_table هو جدول ثنائي الأبعاد حيث نمثل كل حالة بسطر واحد وكل إجراء بعمود واحد. كما نقول أن الحالة هي الموضع الحالي للاعب، لذلك يوجد 16 موضعًا محتملًا في اللعبة لأن الشبكة في البيئة بها كتلة 4 × 4 ، لذلك بها 16 حالة ولدينا 4 إجراءات للقيام بها (أعلى، أسفل، يمين، يسار). لذلك في كل حالة، يمكنني إجراء أحد الإجراءات الأربعة وأحتاج إلى معرفة الإجراء الذي يجب القيام به في حالة معينة تؤدي إلى أقصى مكافأة مستقبلية (الوصول إلى الهدف). لاحظ بعضكم أنه ماذا لو كانت هناك مساحة حالة عالية جدًا (على سبيل المثال، لدي 10 ملايين حالة) فمن المستحيل حلها على هذا النحو. لحسن الحظ، يمكننا حلها باستخدام تقريب الوظيفة وهو المحاضرة التالية. دعنا نعود إلى خوارزمية التعلم Q التي شرحناها في المحاضرة السابقة.

# البيئة 
env=FrozenLake()#معدل التعلم لخوارزمية Q_value 
lr=0.8#عامل الخصم 
جاما=0.95#epsilon لسياسة epsilon 
epsilon=1#عدد العصور 
=1000#عدد الخطوات التي يمكننا القيام بها في كل لعبة 
num_steps=100#قائمة لحفظ المكافأة في كل لعبة للتحقق من عدد الألعاب التي فزنا بها 
reward_List=[]

لذا نحتاج إلى α وهو معدل التعلم وعامل الخصم 𝑒𝑝𝑖𝑠𝑜𝑑𝑒𝑠 وهو رقم الحلقة التي نشغلها 𝑝𝑜𝑙𝑖𝑐𝑦 و 𝑄 − 𝑓𝑢𝑐𝑛𝑡𝑖𝑜𝑛 والذي حددناه سابقًا. سنضيف أيضًا معلمة أخرى وهي الخطوات وهي عدد الخطوات في كل حلقة وهذا مهم هنا، لذلك إذا استغرق العميل وقتًا طويلاً لإنهاء الحلقة، فإننا ننهيها. قائمة المكافآت لإظهار ما إذا كان العميل يتعلم أم لا.

المجموع (المكافأة مقابل المكافأة في قائمة المكافآت إذا كانت المكافأة == 1)/1000

0.743

كما نرى، فقد فزنا في 743 لعبة من أصل 1000 لعبة، لذا فإن التنفيذ جيد، وتعلم عميلنا كيفية لعب هذه اللعبة دون معرفة أي شيء عن العالم، وتعلم اللعب من خلال التفاعل مع البيئة ومراقبة المكافآت.

def play_game(env,q_tabel): 
    """ 
    هذا للعب لعبة تعتمد على Q_tabel الذي تعلمناه 
    """ 
    state=env.reset() 
    for i in range(15): 
        action=np.argmax(q_tabel[state,:]) 
        obs,reward,done=env.step(action) 
        env.render() 
        if done: 
            if reward==1: 
                print('win') 
                break 
            else: 
                print('loss') 
                break 
        state=obs

الشيء الأخير الذي نحدده هو هذه الوظيفة للعب اللعبة وفقًا لجدول Q الذي تعلمناه من قبل.

ملخص:

في هذه المحاضرة، نقدم خوارزمية التعلم Q والتي تعد خارج سياسة TD. نقوم بتدريب العميل على لعب لعبة FrozenLake دون معرفة النموذج الديناميكي للعالم ومن خلال التفاعل مع البيئة فقط.

ولكن ماذا عن مشكلة العالم الحقيقي حيث تكون مساحة الحالة عالية جدًا، إذن نحتاج إلى تحريف الخوارزمية قليلاً للعمل بكفاءة.
في المحاضرة القادمة، سنقدم تقريب الوظيفة وهي إحدى الطرق لحل هذه المشكلة.

آمل أن تجد هذه المقالة مفيدة وأنا آسف للغاية إذا كان هناك أي خطأ أو خطأ إملائي في المقالة، فلا تتردد في الاتصال بي، أو ترك تعليق لتصحيح الأمور.

خليل حنارة
مهندس ذكاء اصطناعي في مسراج