سنقدم في المحاضرة الأخيرة كيفية تعلم سياسة جيدة من التجربة. لكننا افترضنا أنه يمكننا تمثيل دالة القيمة 𝑉 ( 𝑠 )، 𝑄 ( 𝑠 , 𝑎 ) كمتجه ومصفوفة (تمثيل جدولي). كما ذكرنا في المحاضرة السابقة، فإن العديد من العوالم الحقيقية بها مساحات حالة و/أو فعل هائلة . لذا فإن التمثيل الجدولي غير كافٍ . يمكننا حل هذه المشكلة باستخدام تقريب دالة القيمة (VFA) . سنمثل دالة 𝑄 و𝑉 بدالة ذات معلمات بدلاً من دالة شبيهة بالجدول (الشبكة العصبية، الدالة الخطية، إلخ.) .

تم وصف جميع طرق التنبؤ التي تمت تغطيتها في المحاضرة السابقة على أنها تحديثات لدالة القيمة المقدرة التي تحول قيمتها في حالات معينة نحو "قيمة احتياطية" أو هدف تحديث لتلك الحالة. دعنا نشير إلى تحديث فردي بالترميز 𝑠 ↦ 𝑢 ، حيث 𝑠 هي الحالة المحدثة و𝑢 هو هدف التحديث الذي يتم تحويل القيمة المقدرة لـ s نحوه. على سبيل المثال، تحديث مونت كارلو للتنبؤ بالقيمة هو 𝑆𝑡 ↦ 𝐺𝑡 ، وتحديث TD(0) هو 𝑆 ₜ↦ 𝑅 ₜ₊₁+ 𝛾𝑄 ( 𝑆 ₜ₊₁, 𝑤 ₜ). في تحديث تقييم سياسة البرمجة الديناميكية (DP)، 𝑠 ↦ 𝐸 [ 𝑅 ₜ₊₁+ 𝛾𝑄 ( 𝑆 ₜ₊₁, 𝑤 ₜ)| 𝑆 ₜ= 𝑠 ]، يتم تحديث حالة عشوائية 𝑠 ، بينما في الحالات الأخرى يتم تحديث الحالة التي تم مواجهتها في التجربة الفعلية، 𝑆 ₜ.

من الطبيعي تفسير كل تحديث على أنه يحدد مثالاً لسلوك الإدخال والإخراج المطلوب لدالة القيمة. بمعنى ما، يعني التحديث 𝑠 ↦ 𝑢 أن القيمة المقدرة للحالة 𝑠 يجب أن تكون أشبه بهدف التحديث u. حتى الآن، كان التحديث الفعلي تافهًا: تم ببساطة نقل إدخال الجدول للقيمة المقدرة 𝑠 بمقدار جزء بسيط من الطريق نحو 𝑢 ، وتركت القيم المقدرة لجميع الحالات الأخرى دون تغيير. الآن نسمح لأساليب معقدة ومتطورة بشكل تعسفي بتنفيذ التحديث، والتحديث عند 𝑠 يعمم بحيث تتغير القيم المقدرة للعديد من الحالات الأخرى أيضًا. تسمى طرق التعلم الآلي التي تتعلم محاكاة أمثلة الإدخال والإخراج بهذه الطريقة أساليب التعلم الخاضع للإشراف ، وعندما تكون المخرجات أرقامًا، مثل 𝑢 ، غالبًا ما تسمى العملية تقريب الدالة . تتوقع طرق تقريب الدالة تلقي أمثلة على سلوك الإدخال والإخراج المطلوب للدالة التي تحاول تقريبها. نستخدم هذه الطرق للتنبؤ بالقيمة ببساطة عن طريق تمرير 𝑠 ↦ 𝑔 لكل تحديث إليها كمثال تدريبي. ثم نفسر الدالة التقريبية التي تنتجها كدالة قيمة تقديرية.

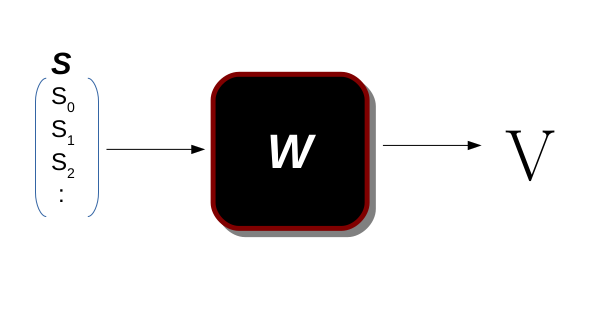
𝑆 هو متجه الحالة (متجه الميزة) ، و𝑊 هو المعامل الذي يمثل الدالة و𝑉 هي دالة القيمة للحالة 𝑠 ، وفي هذه الدالة، نقوم بالتحويل من الحالة إلى قيمة تلك الحالة 𝑉 ( 𝑠 )= 𝑡 ؛ 𝑡 ∈ 𝑅

يمكننا أيضًا استخدام VFA لتعلم دالة 𝑄 .

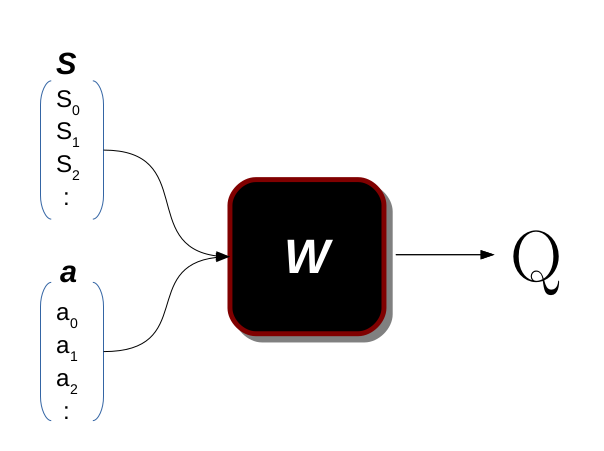
في 𝑄 ( 𝑠 , 𝑎 ) نقوم بتعيين الزوج ( 𝑠 , 𝑎 ) إلى القيمة. في عالم آخر، نقول ما هي أهمية اتخاذ الإجراء 𝑎 في الحالة 𝑠 .

فوائد VFA.

• الأهم هو التعميم كإنسان يحب تعميم جميع المشاكل التي يواجهها، فنحن نسعى إلى جعل الكمبيوتر لديه هذه المهارة. (على سبيل المثال، إذا رأى الإنسان بابًا واحدًا أو بابين، فسوف يتعرف على أي أنواع من الأبواب التي سيرونها في المستقبل، ولكن بالنسبة لأجهزة الكمبيوتر، فإنها تحتاج إلى العديد من الأمثلة لتعلم ذلك، ولكن إذا كان بإمكانها التعرف عليها، فقد صنعنا نموذجًا جيدًا). ​​في حالتنا، نريد أن يتعلم العميل اتخاذ إجراء في حالة ما حتى لو لم يسمع بها من قبل.
• تقليل الذاكرة، إذا استخدمنا دالة ذات معلمات بدلاً من التمثيل الجدولي، فسنقوم بتقليل استخدام الذاكرة إذا كانت مساحة الحالة و/أو الإجراء هائلة. (على سبيل المثال، إذا كان هناك 1∗10⁶ حالة و50 إجراء، فأنا بحاجة إلى جدول يحتوي على (50∗10⁶)) إدخالات وهذا كثيرًا بينما يمكنني استخدام المعلمة 10⁴ لتقريب هذه الدالة.
• تقليل الحساب في معظم الحالات، (على سبيل المثال إذا أخذنا المثال السابق حيث نحتاج إلى (50∗10⁶) إدخالات) لحل هذه المشكلة باستخدام خوارزمية 𝑄 − 𝑙𝑒𝑎𝑟𝑛𝑖𝑛𝑔 التي نحتاجها لكل تكرار 𝑂 ( 𝑁 ²) والتي تساوي ∼10¹².

التعلم العميق Q

بعد أن قدمنا ​​بإيجاز VFA، سننفذ إحدى أكثر الأوراق البحثية شيوعًا في السنوات العشر الماضية. في هذا القسم، سننفذ خوارزمية التعلم العميق Q (DQN) باستخدام بيئة OpenAI وأطر عمل Tensorflow . يقدم " Mnih، إلخ. لعب Atari باستخدام التعلم التعزيزي العميق 2013". DQN لأول مرة. يقوم المؤلفون في هذه الورقة بتدريب وكيل على تشغيل ألعاب Atari 2600 من وحدات البكسل الخام وكان ذلك مذهلاً لأن الوكيل لا يعرف شيئًا عن البيئة أو دور الألعاب على الرغم من أنه يمكنه اللعب كإنسان أو حتى أفضل لبعض الألعاب.

أوصي بشدة بقراءة هذه الورقة لأنها بسيطة للغاية وسهلة الفهم، وسوف تجعل قراءة الأوراق المستقبلية أسهل.

ملحوظة : يرجى قراءة هذا القسم بعناية، يجب أن تفهم كل التفاصيل لأننا سنعيد استخدام الكود من هذا القسم في المحاضرات المستقبلية.

#استيراد مكتبة التبعيات# مكتبة البيئة 
استيراد صالة الألعاب الرياضية#إطار عمل الذكاء الاصطناعي 
استيراد tensorflow كـ tf 
استيراد tensorflow.keras كـ keras 
استيراد numpy كـ np#فقط لرسم الأشياء 
استيراد cv2 
استيراد matplotlib.pyplot كـ plt 
استيراد tqdmمن المجموعات استيراد deque

بعد أن نقوم باستيراد التبعيات سنقوم بإنشاء بيئتنا باستخدام مكتبة Gym ، وقد اخترنا لعبة Breakout كلعبة ملعب.

# قم بإنشاء البيئة التي اخترناها للعبة Breakout لتجربتها. 
environmental=gym.make("Breakout-v4") 
state=environment.reset() 
plt.imshow(state)

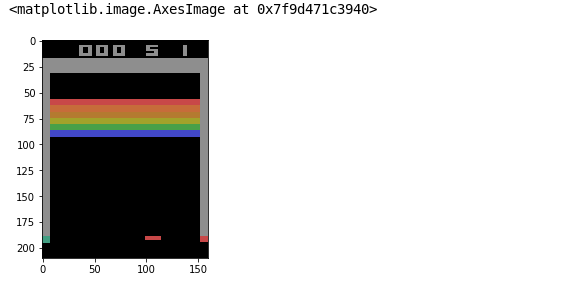
الخطوة الأولى هي إجراء بعض التعديلات على كل إطار، نريد تغيير تنسيق RGB إلى تنسيق رمادي وهذا يقلل من الارتباك في الشبكة وسنقطع الجزء العلوي من الإطار الذي يمثل النتيجة التي تتغير وقد تربك عملية التدريب.

def preprocess_frame(frame): 
    image=frame[25:-10,5:-5,:] 
    image=tf.image.rgb_to_grayscale(image) 
    image=tf.image.resize(image,[84,84]) 
    image=tf.reshape(image,[85,85]) 
    image=image/255.0 
    إرجاع الصورةdef ploting_function_one(frame): 
    image=frame[25:,:,:] 
    image=cv2.cvtColor(image,cv2.COLOR_RGB2GRAY) 
    image=cv2.resize(image,(85,85)) 
    إرجاع الصورة

تقوم هذه الوظيفة بخطوات المعالجة المسبقة لكل إطار من اللعبة.

المعلمة:

• الإطار: هو إطار صف بحجم [210 * 64 * 3] توفره لنا البيئة بعد أن نقوم بإجراء يغير العالم، وتوفر لنا البيئة ملاحظات جديدة بعد تطبيق هذا الإجراء.

يعود :

• الصورة: إطار المعالجة حيث نقوم بقص بعض الحدود والحفاظ على منطقة اللعب وتغيير الصورة إلى تدرج الرمادي ثم إعادة حجمها إلى شكل [84، 84] وأخيرًا تطبيع قيمة البكسل لتصبح في النطاق [0–1]

تحتوي الخلية أعلاه على دالتين للمعالجة المسبقة، واحدة للتصور لأننا لا نستطيع رسم الموتر من TensorFlow

class FireResetEnv(gym.Wrapper): 
    def __init__(self, env=None): 
        super(FireResetEnv, self).__init__(env) 
        assert env.unwrapped.get_action_meanings()[1] == 'FIRE' 
        assert len(env.unwrapped.get_action_meanings()) >= 3 
        
    def step(self, action): 
        return self.env.step(action) 
    
    def reset(self): 
        self.env.reset() 
        obs, _, done, _ = self.env.step(1) 
        إذا تم ذلك: 
            self.env.reset() 
            obs, _, done, _ = self.env.step(2) 
            إذا تم ذلك: 
                self.env.reset() 
        return obs

هذه الفئة هي Wrapper حيث نتأكد من تشغيل اللعبة، لأنه في بعض البيئات في مكتبة الصالة الرياضية يجب أن تبدأ اللعبة بالإجراء "1" في معظم اللعبة، لذلك من خلال القيام بذلك نتأكد من تشغيل اللعبة.

الآن بعد معالجة الإطار، نحتاج إلى تكديس بعض الإطارات معًا لتمثيل حالة واحدة، وبالتالي يمكننا استخدام ذلك لإعطاء بعض المعلومات حول السرعة. أولاً، دعنا ننشئ قائمة انتظار بحجم ثابت 4، لذلك بعد كل حركة، ندفع الإطار إلى قائمة الانتظار ثم نكدسهما معًا لتمثيل الكتلة ثلاثية الأبعاد التي تمثل الحالة. الآن بعد معالجة الإطار، نحتاج إلى تكديس بعض الإطارات معًا لتمثيل حالة واحدة، وبالتالي يمكننا استخدام ذلك لإعطاء بعض المعلومات حول السرعة.

الكتل المكدسة=deque(الحد الأقصى=4)def state_creator(frame,is_new_episod,stacked_blocks,number_of_frame=4): 
    إذا كانت الحلقة الجديدة: 
        image=preprocess_frame(frame) 
        بالنسبة إلى i في النطاق(number_of_frame): 
            stacked_blocks.append(image) 
    وإلا: 
        image=preprocess_frame(frame) 
        stacked_blocks.append(image) 
    
    state=tf.stack(stacked_blocks,axis=2) 
    إرجاع الحالة

في هذه الوظيفة، نقوم بتكديس الإطارات الأربعة الأخيرة معًا لأداء حالة واحدة، وهذا يمنحنا بعض الحدس حول السرعة.

المعلمة :

• الإطار: وهو ملاحظة اللعبة.
• is_new_episod: معلمة منطقية تتحقق مما إذا كان هناك إطار سابق وما حدث في بداية كل حلقة.
• stacked_blocks: هي كتلة بها أقصى طول 4 تحفظ لنا الإطارات الأربعة الأخيرة.
• number_of_frame: هو افتراضيًا 4 ولكن يمكننا تغييره إلى رقم آخر مما يجعل حالتنا أكثر تعقيدًا.

يعود :

• الحالة: موتر ذو شكل [84,84,4] يمثل حالة عالمنا.

الآن دعنا نبني النموذج الذي هو عبارة عن شبكة عصبية ملتوية تحتوي على طبقتين فقط. ستأخذ الشبكة العصبية الملتوية حالة هي الموتر [84,84,4] ويكون متجه الإخراج بنفس بُعد مساحة الفعل. هذا يعني أنه بالنسبة لكل حالة سأتعلم مدى أهمية اتخاذ كل إجراء في تلك الحالة دفعة واحدة.

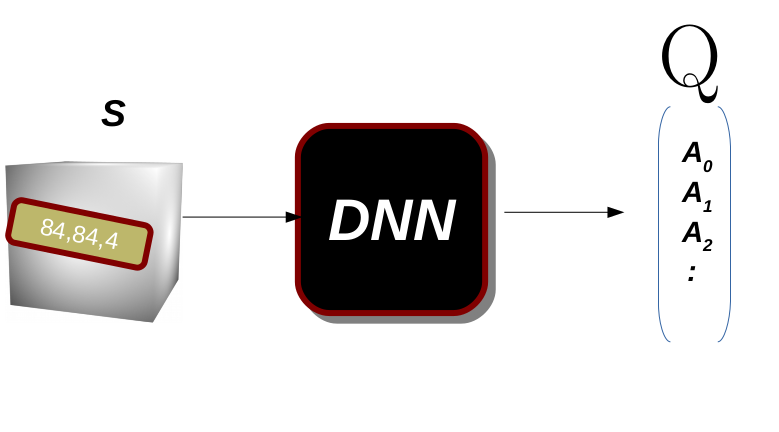
كما نرى في الشكل ، سيتعلم النموذج أهمية جميع الإجراءات لكل حالة، لذلك إذا اتخذنا الإجراء ذو ​​القيمة الأعلى، فيجب أن يؤدي ذلك إلى أفضل مكافأة.

#هذا النموذج موصى به من ورقة "Mnih 2013، لعب Atari مع التعلم التعزيزي العميق" 
keras.backend.clear_session()النموذج = keras.Sequential ([ 
    keras.layers.Conv2D (16، 8، strides = 4، padding = 'صالح'، التنشيط = 'relu'، شكل الإدخال = [84، 84، 4])، 
    keras.layers.Conv2D (32، 4، strides = 2، padding = 'صالح'، التنشيط = 'relu')، 
    keras.layers.Flatten ()، 
    keras.layers.Dense (256، التنشيط = 'relu')، 
    keras.layers.Dense (مساحة العمل) 
]) 
نموذج الملخص ()

بدلاً من تدريب DQN بناءً على أحدث التجارب فقط، سنخزن جميع التجارب في مخزن إعادة التشغيل (أو ذاكرة إعادة التشغيل)، وسنأخذ عينة من دفعة تدريب عشوائية منها في كل تكرار تدريب. يساعد هذا في تقليل الارتباطات بين التجارب في دفعة التدريب، مما يساعد التدريب بشكل كبير.

# يمثل هذا الذاكرة التي نحتفظ فيها بالمليون حالة الأخيرة للتدريب. 
replay_buffer=deque(maxlen=1000000)def sample_experiences(batch_size): 
    indices=np.random.randint(len(replay_buffer),size=batch_size) 
    batch=[replay_buffer[index] for index in indices] 
    states,actions,rewords,dones,next_states=[np.array([experiance[field_index] for experiance in batch]) for field_index in range(5)] 
    return states,actions,rewords,dones,next_states

يتم استخدام هذه الوظيفة لأخذ عينات من الدفعة من ذاكرتنا.

المعلمة :

• حجم الدفعة: هو عدد الأمثلة المقدمة لشبكتنا.

يعود:

• الحالات: إنه tensore [batch_size, image_width, image_height, stacked_size] في حالتنا [32, 84, 84, 4]
• الإجراءات: إنها مصفوفة ثنائية الأبعاد [batch_size, action] وهي الإجراء في كل حالة في الدفعة الخاصة بنا
• المكافآت: إنها مصفوفة ثنائية الأبعاد [batch_size, reward] وهي المكافأة في كل حالة في الدفعة الخاصة بنا
• dones: إنها مصفوفة ثنائية الأبعاد [batch_size, done] حيث أن done هي قيمة منطقية تساعدنا في حساب الهدف.
• next_state: إنه tensore [batch_size, image_width, image_height, stacked_size] في حالتنا [32, 84, 84, 4]

𝜖−𝑔𝑟𝑒𝑒𝑑𝑦

خوارزمية

لقد ذكرنا من قبل 𝜖 − 𝑔𝑟𝑒𝑒𝑑𝑦 في المحاضرة [3]، الكود الزائف للخوارزمية هو كما يلي والدالة epsilon_greedy_policy هي مجرد تنفيذ لهذه الخوارزمية.

• ← 1
• 𝑎 ← 𝑟𝑎𝑛𝑑𝑜𝑚 − 𝑣𝑎𝑙𝑢𝑒 ∈[0,1]
• 𝑖𝑓𝑎 < 𝜖
• خذ عشوائيًا 𝑎 ∈ 𝐴
• 𝑒𝑙𝑠𝑒
• اختار الفعل الجشع باستخدام المقدر (على سبيل المثال 𝑎𝑟𝑔𝑚𝑎𝑥𝑎𝑄 ( 𝑠 , 𝑎 ))
• 𝜖 ← 𝑢𝑝𝑑𝑎𝑡𝑒

def epsilon_greedy_policy(state,epsilon): 
    إذا كان np.random.rand()<epsilon: 
        ارجع np.random.randint(action_space) 
    وإلا: 
        Q_values=model.predict(state[np.newaxis]) 
        ارجع tf.argmax(Q_values[0])
def play_one_step(env,state,epsilon): 
  
    action=epsilon_greedy_policy(state,epsilon) 
    next_state,reward,done,info=env.step(action) 
    if info['ale.lives']< 5: 
            done=True 
    stacked_next_state=state_creator(next_state,False,stacked_blocks) 
    replay_buffer.append((state,action,reward,done,stacked_next_state)) 
    return stacked_next_state,reward,done,info

تعمل وظيفة Play one step على إجراء والحصول على الملاحظة من العالم. نقوم بإجراء إجراء ثم نحصل على الملاحظة الكاملة من بيئتنا عن طريق تطبيق وظيفة state_create على الملاحظة (الإطار) ثم نحفظها في الذاكرة لخطوة التدريب.

المعلمة :

• env: يمثل عالمنا أو البيئة التي نعمل عليها
• الحالة: هي الحالة الحالية.
• إبسيلون: هو الحد الذي نستخدمه لاختيار الفعل

يعود :

• next_state: كتلة tensor [84,84,4] تمثل الإطارات الأربعة الأخيرة.
• المكافأة: رقم عائم وهو المكافأة التي نحصل عليها بعد القيام ببعض الإجراءات.
• تم: إنه أمر منطقي يشير إلى ما إذا كانت اللعبة قد انتهت أم لا
• المعلومات: قاموسه يحتوي على عداد الأرواح.

دالة الخسارة = tf.losses.mean_squared_error 
المُحسِّن = tf.optimizers.Adam(lr=0.00025)

نحن نستخدم خطأ التربيع المتوسط ​​كدالة خسارة ومحسن Adam، ويستخدم المؤلفون في [1] RMSprop بدلاً من ذلك، ولكن نظرًا لأن Adam أقل حساسية لحجم الخطوة، فمن الأفضل استخدامه.

في المحاضرة 3، قدمنا ​​خوارزمية 𝑄 − 𝑙𝑒𝑎𝑟𝑛𝑖𝑛𝑔 وفي المحاضرة السابقة قمنا بتنفيذها، دعونا أولاً نعود إلى الخوارزمية.

ولكن هنا نستخدم تقريب الدالة، وليس التمثيل الجدولي. لذا كما قلنا في القسم الأول، سنستخدم العائد كهدف لنموذجنا. نذكر قبل ذلك 𝑇𝐷 − 𝑡𝑎𝑟𝑔𝑒𝑡 = 𝑅 ₜ+ 𝛾𝑉 ( 𝑠 ₜ₊₁) وهذا ما سنستخدمه هنا كهدف لنموذجنا. بمعنى ما، يعني التحديث 𝑠 ↦ 𝑢 أن القيمة المقدرة للحالة 𝑠 يجب أن تكون أشبه بهدف التحديث 𝑢 ، وفي عالم آخر سيحاول النموذج تقليل الفرق بين قيمة الحالة الحالية وقيمة العائد من الحالة التالية وهذا صحيح لأنه إذا كنا نستخدم الإجراء الأمثل في كل حالة، فيجب أن تكون قيمة كل حالة قريبة من بعضها البعض.

def training_step(batch_size,discount_factor): 
    #تجربة عينة من مخزن الإعادة 
    # states → s، next states → s'، rewards → r، actions → a. في الخوارزمية أعلاه. 
    states,actions,rewards,dones,next_states=sample_experiences(batch_size) 
    
    #max′a Q(s′,a′) 
    next_Q_values=model.predict(next_states) 
    max_next_Q_values=np.max(next_Q_values,axis=1) 
    # [r + gamma * max′a Q(s′,a′)] 
    target_Q_values=rewards+(1-dones)*discount_factor*max_next_Q_values 
    ​​# سيساعدنا هذا القناع في تقليل قيمة النموذج إلى مجرد الإجراء الذي قمنا به. 
    mask = tf.one_hot(actions, action_space) 
    # ابدأ بحساب التدرج 
    باستخدام tf.GradientTape() كشريط: 
        # Q(s,a) 
        all_Q_values=model(states) 
        # هذه الخطوة هي لاختيار الإجراء الذي نقوم به فقط وليس كل الإجراءات لكل حالة. 
        Q_values=tf.reduce_sum(all_Q_values*mask,axis=1,keepdims=True) 
        # [r + gamma * max′a Q(s′,a′)] - Q(s,a) 
        loss=tf.reduce_mean(loss_function(target_Q_values,Q_values)) 
    # احسب التدرج لمتغيرات النموذج 
    gradiants=tape.gradient(loss,model.trainable_variables) 
    # قم بخطوة التحسين. 
    optimizer.apply_gradients(zip(gradiants,model.trainable_variables))

هذه الوظيفة مسؤولة عن القيام بخطوة تدريب واحدة حيث نقوم بأخذ عينة من دفعة واحدة من مخزن الإعادة ثم ندفع هذه الدفعة في نموذجنا للخطوة الأمامية ونطبق التدرج باستخدام المحسن يدويًا.

المعلمة :

• batch_size: عدد أمثلة التدريب التي نقوم بأخذ عينات منها
• discout_factor: هذه المعلمة مسؤولة عن المكافآت المستقبلية، ومن المهم أن تكون قيمتها في النطاق [0–1]

يعود:

• لا يوجد، حيث يتم تطبيق التغيير في مكان معلمة النموذج.

الخطوة الأخيرة هي إنشاء حلقة التدريب، وسوف نستخدم الدالة التي أنشأناها أعلاه.

الحلقات=700 
إبسيلون=1.0 
حجم الدفعة=5 
عامل الخصم=0.98للحلقة في tqdm.tqdm(range(episodes)): 
    state=environment.reset() 
    stacked_state=state_creator(state,True,stacked_blocks) 
    rewards=0 
    epsilon=max(1-episode/500,0.1) 
    while True: 
        stacked_state,reward,done=play_one_step(environment,stacked_state,epsilon) 
        rewards+=reward 
        if done: 
            if not (episode%10): 
                print(rewards) 
            break 
            
        if len(replay_buffer)>50: 
            training_step(batch_size,discount_factor)

الآن دعونا نضع كل ذلك معًا في فصل واحد، يمكنك التحقق من الكود الكامل على Github.

أقوم بإنشاء فئة DQN_Agent التي ستغلف جميع الوظائف المذكورة أعلاه وأوفر لها المعلمات الافتراضية كما هو الحال في الورقة التي قمنا بتنفيذها.

𝑁𝑜𝑡𝑒 : في المحاضرات القادمة، سنقوم فقط بتحرير هذه الفئة، وسأشير إلى سطر التحرير بعلامة ⟶.

ملخص:

في هذه المحاضرة نقدم تقريب الوظيفة وهو مفهوم قوي جدًا في مجال التعلم الآلي والذكاء الاصطناعي بشكل عام، كما ننفذ أيضًا خوارزمية Deep 𝑄 − 𝑙𝑒𝑎𝑟𝑛𝑖𝑛𝑔 للعب لعبة Breakout.

آمل أن تجد هذه المقالة مفيدة وأنا آسف للغاية إذا كان هناك أي خطأ أو خطأ إملائي في المقالة، فلا تتردد في الاتصال بي، أو ترك تعليق لتصحيح الأمور.

خليل حنارة
مهندس ذكاء اصطناعي في مسراج